The IMDB 5000 Movie Dataset is an IMDB movie dataset obtained by scraping movie review data from the Internet Movie Database. It is a very rich dataset and I will only scratch the surface of what can be learned from it with exploratory data analysis.
Let’s start to see where the movies come from:
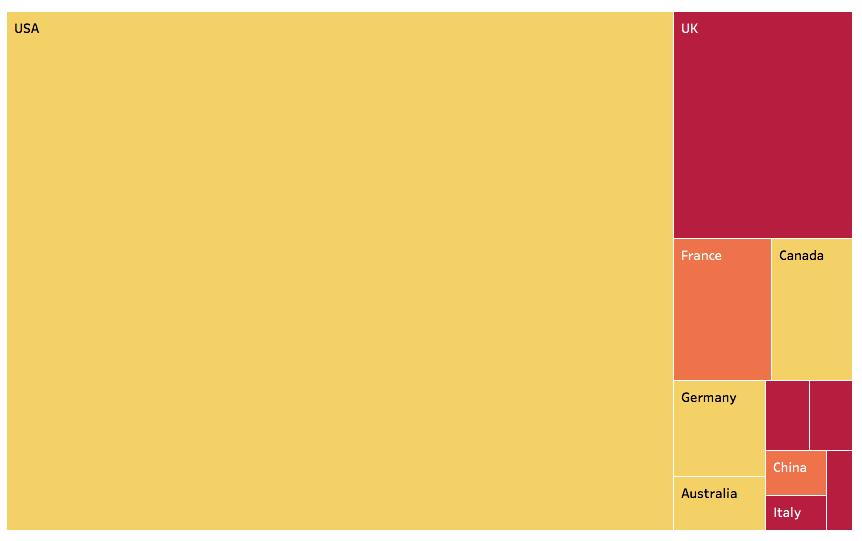
Size of the rectangles is the number of movies in the IMDB movie dataset. Color codes the IMDB score. They make great movies in Italy (dark red, bottom right) but few of them.
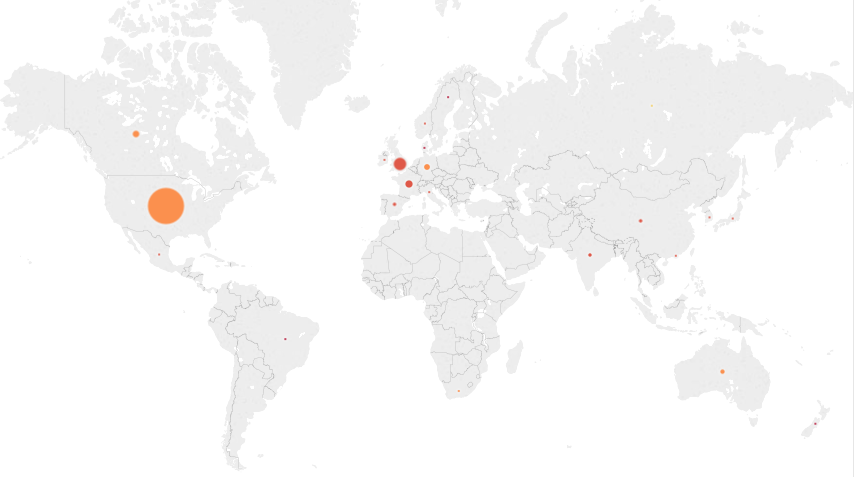
The movies in the dataset come mostly from the US and other english speaking countries. If we do not filter the dataset, we will be learning mostly about this market. This is another view:
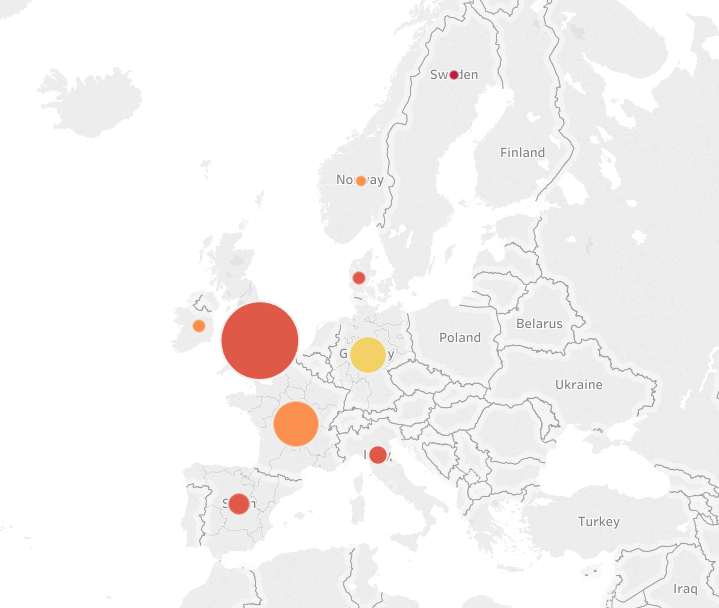
Colors still encode IMDB rating, and the size of the symbols is proportional to the number of movies. Many countries produce movies in Europe (by the way, I am not displaying countries with less than twenty movies) but not many of them, so it’s difficult to see what’s going on in Europe at this scale. Let’s zoom in:
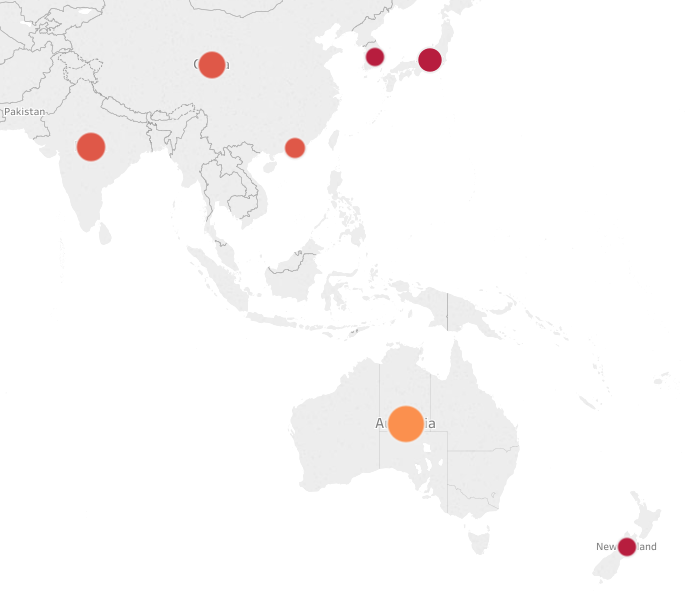
The UK dominates, as we saw also from the first plot. Zoom in for Asia-Pacific:
Now let’s try to understand which factors affect the box-office gross of a movie. This is likely the most interesting parameter from a business point of view and being able to predict it accurately would be invaluable.
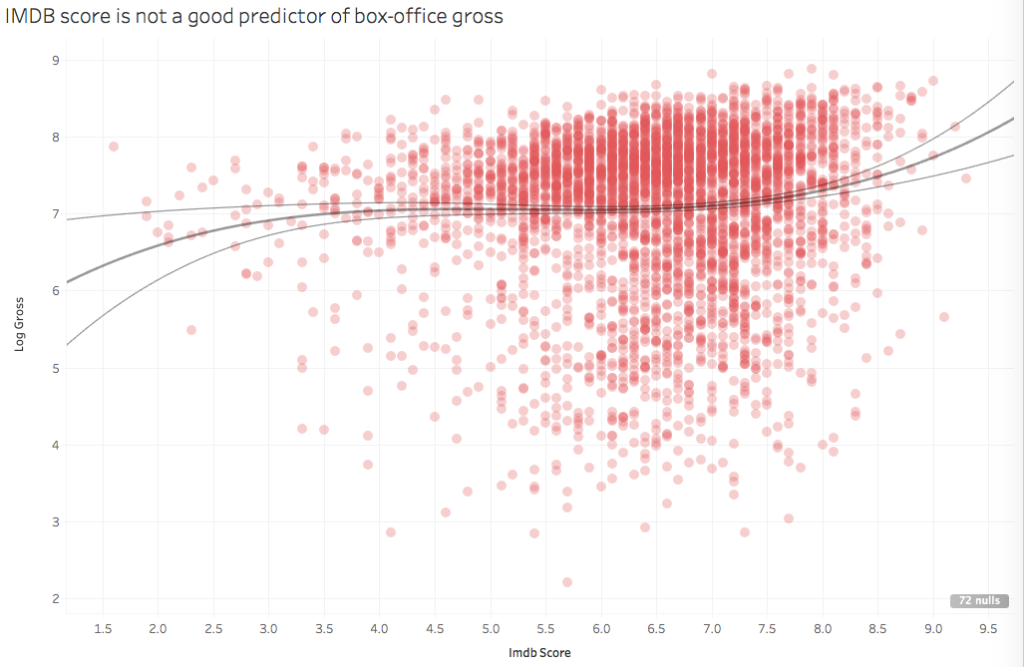
First off, IMDB score is not a good predictor of box-office gross:
Log box-office gross (base 10) is on the y-axis. I took the log because as you see movie grosses vary by about seven orders of magnitude: from grocery-shopping bill to small-country GDP.
I let Tableau add a polynomial trend line (it finds a third degree polynomial), but the quoted R-squared is ~0.01. I could work on this in R to see if any improvement can be had, but by eye it’s clear that the IMDB score isn’t very useful, at least at this stage. Here’s a better predictor:
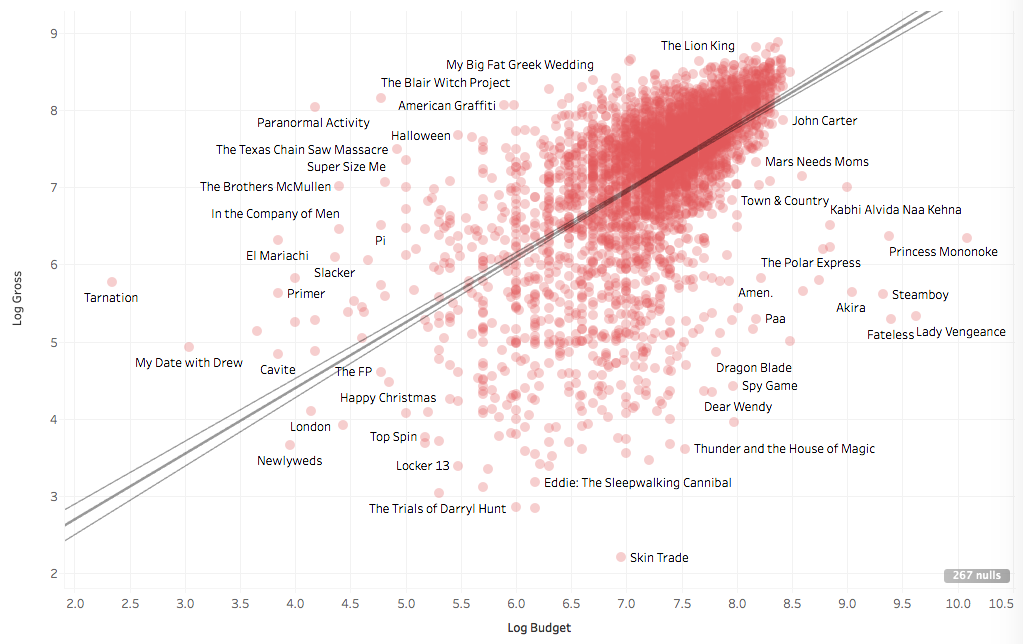
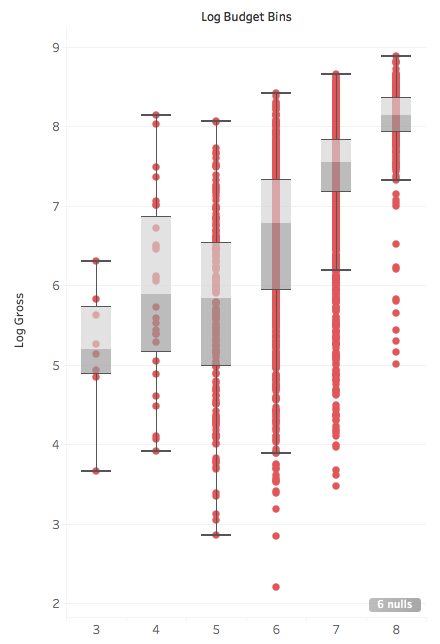
Log budget of the movie seems to be in a linear relation with log gross. The R-square is about 0.3, which is decent but surely not exciting (roughly speaking about 30% of the variance in the log gross is accounted for by its correlation with log budget). So a first rough idea of the expected box-office gross of a movie can be had using a power-law relation with its budget. Another way to see this:
Budget definitely affects the box-office gross. What about the total number of Facebook likes of the whole crew?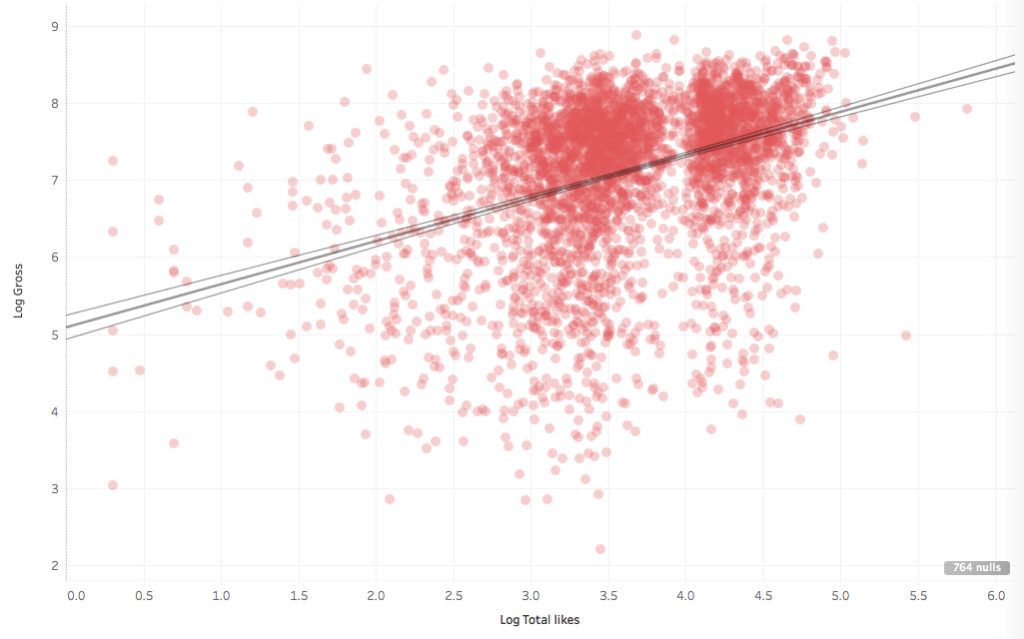
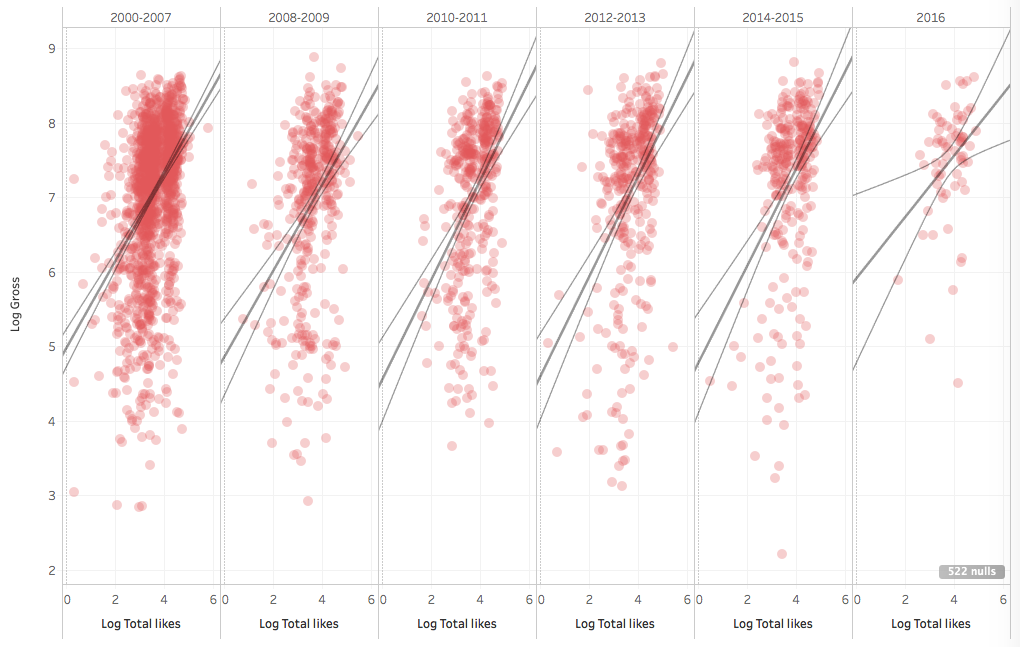
Yes, there is some correlation between the log total likes (I took the log because likes vary a lot, like money: this is clearly an Extremistan dataset). I wonder if the correlation would improve by breaking down the dataset by year: social-media related metrics may depend strongly on time.
Well, no. There doesn’t seem to be much of an effect. Surely the correlation between Facebook likes and gross is interesting and should be looked into. I’d switch to R and try more transforms and run some regression diagnostics. Also why are the likes clustered in two big groups with a gap at around 10000 likes?
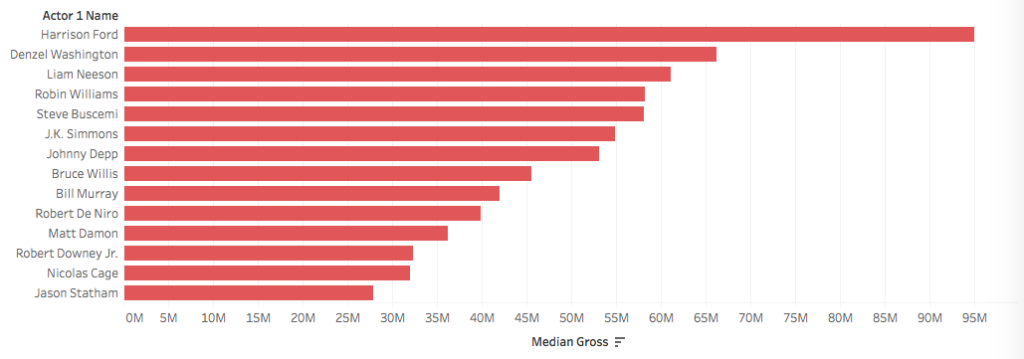
Let’s see now how the human factor affect the box office gross. I defined famous actors as those who appear as lead actor in more than 25 movies in the dataset. Here they are with the median gross of their movies (length of the horizontal bar):
As this is the median of at least 25 datapoints for each actor, we see that big-name actors consistently affect the bottom line. Is it just because they star in big budget movies, which -as we saw- tend to have higher box-office gross, or is there more?
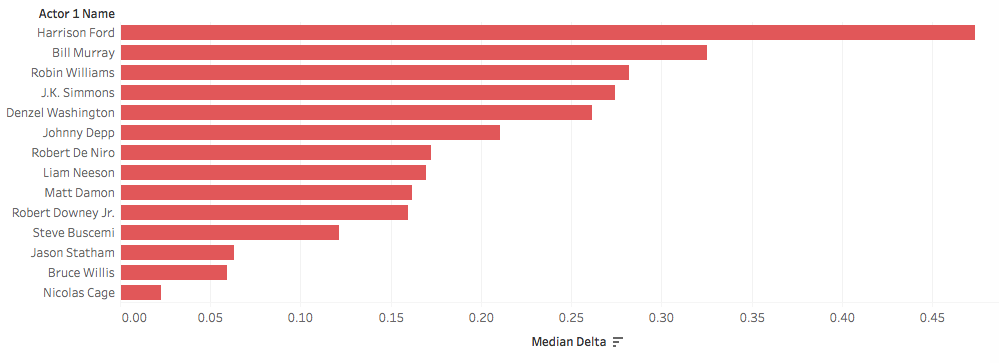
It’s easy to check this by using the trend between log budget and log gross that we saw before. I predicted the box office gross based only on the budget, and I called delta the difference between the actual and predicted gross. So a movie with a positive delta earned more in the box office than expected based on its budget. This way we can see how actors affect delta:
It is clear that famous actors affect the ability of a movie to earn more than the prediction based merely on the budget figure. In other words (and in a very rough first approximation) it is worth cutting into the budget to hire a big-name actor.
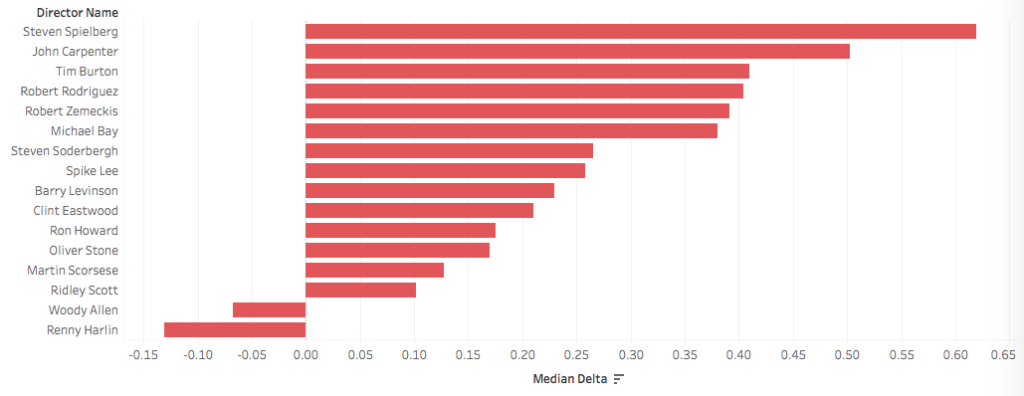
Is it the same for directors?
It is, with a few exceptions. Famous directors increase the median box-office gross of a movie over the prediction from the budget.
Note that the two exceptions are most likely due to the fact that the model for box-office gross is very rough: there are other features that affect the box-office gross in addition to the budget. Don’t fire Woody Allen yet.